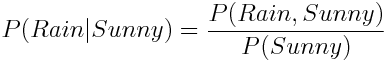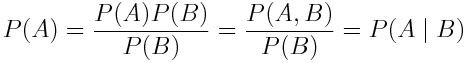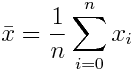Теория вероятностей для самых маленьких

Вероятности
Зачем нам нужны вероятности, когда мы обладаем таким мощным математическим инструментарием? У нас есть матанализ для работы с функциями на бесконечно малых величинах и оценки их динамики. У нас есть алгебра для решения уравнений, а также десятки других областей математики, с помощью которых мы можем решить едва ли не любую задачу.
Проблема в том, что мы живем в хаотичной вселенной, где точные измерения чаще всего невозможны. Изучая реальные процессы, происходящие в мире, мы хотим понять, какие случайные события влияют на наши эксперименты. Нас окружает неопределенность, и важно уметь «обуздать» и использовать ее в своих целях. Именно в такие моменты в ход идет теория вероятностей и статистика.
В наш век именно эти дисциплины лежат в основе искусственного интеллекта, физики элементарных частиц, обществознания, биоинформатики.
Перед тем как говорить о статистике, необходимо определиться с понятием вероятности. Как ни странно, однозначного ответа нет. Рассмотрим несколько теоретических подходов к определению вероятности.
Частотная вероятность
Представим, что нам дали монету, и мы хотим определить является ли она честной. Как это можно сделать? Подбросим ее несколько раз и запишем как 1, если выпадет орёл, 0 – если выпадет решка. Повторим этот эксперимент 1000 раз, и подсчитаем все 0 и 1. Допустим, по результатам этого утомительного процесса мы насчитали 600 орлов (1) и 400 решек (0). Если мы посчитаем частоту, с которой нам выпадал орёл или решка, мы получим 60% и 40%, соответственно. Эти частоты могут интерпретироваться как вероятности того, что, подбросив монету, нам выпадет орёл или решка. Такой подход к вероятностям называется частотным.
Условные вероятности
Зачастую нам нужно узнать вероятность наступления события при условии, что произошло другое событие. В этом случае, мы указываем условную вероятность события A при условии, что произошло событие B как P (A | B). Рассмотрим это на примере дождя:
· Какова вероятность дождя, если мы слышим раскаты грома?
· Какова вероятность дождя, если на улице солнце?
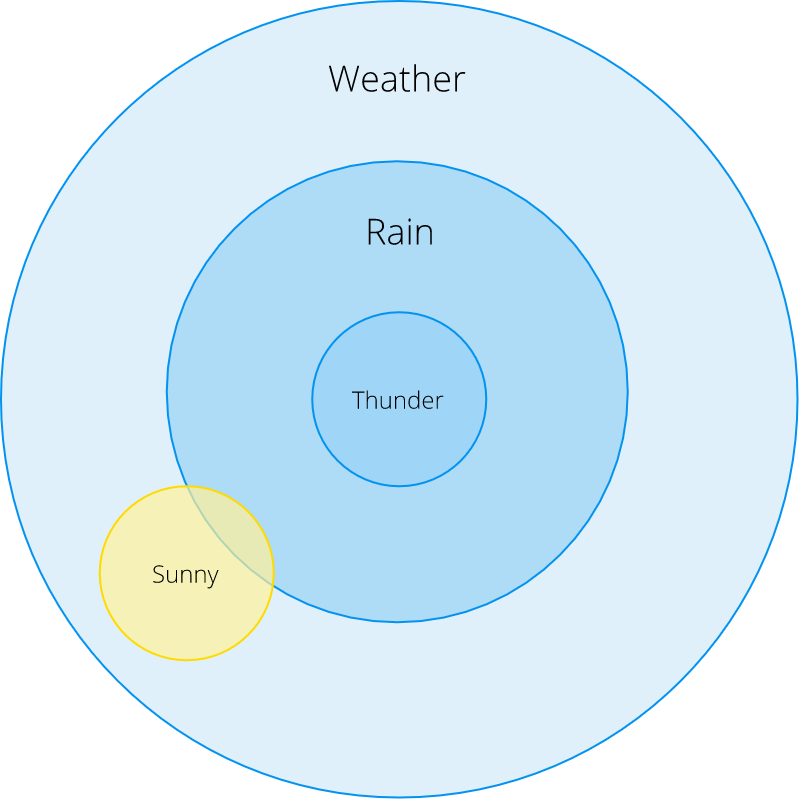
Из этой диаграммы Эйлера мы видим, что P (Дождь | Гром) = 1: дождь идет всегда, когда мы слышим раскаты грома и видим молнии (в реальности это не всегда так, но примем условности для целей нашего примера).
А что насчет P (Дождь | Солнце)? На глаз, эта вероятность достаточно мала, но есть ли способ рассчитать ее точно? Условная вероятность определяется как:
Иными словами, мы должны поделить вероятность наступления обоих событий – Дождя и Солнечной погоды на вероятность события Солнечная погода.
Зависимые и независимые события
События называются независимыми, если вероятность наступления любого из них никак не зависит от наступления других событий. Например, рассмотрим вероятность того, чтобы бросить игральные кости и выкинуть две двойки подряд. Это независимые события. Иными словами,
![]()
Но почему эта формула работает? Для начала обозначим броски №1 и №2 как A и B, чтобы упростить формулу, а далее перепишем вероятность бросания костей как вероятность появления двух независимых событий:
![]()
Затем умножим P(A) на P(B) / P(B), а далее вспомним определение условной вероятности:
Если формулу выше прочитать справа налево, мы увидим, что P (A | B) = P(A). По сути, это означает, что событие A не зависит от события B. Такая же логика справедлива и в отношении P(B).
Байесовский подход к вероятности
Существует еще один подход к определению вероятностей, который называется Байесовским. Частотный подход к статистике предполагает существование одной оптимальной и конкретной комбинации параметров для модели. Частотная статистика работает с неопределенностью через достаточно сложные для понимания доверительные интервалы (confidence interval). К примеру, 95% доверительный интервал в частотной статистике означает, что если бы мы проводили измерение бесконечное количество раз, то истинное значение параметра попадало бы в этот интервал в 95% случаев. Сбивает с толку, да?
С другой стороны, Байесовская теорема подходит к параметрам с вероятностных позиций и рассматривает их как случайные величины. В Байесовской статистике каждый параметр обладает собственным распределением вероятности, которое отражает, насколько вероятны данные параметры, учитывая имеющиеся в наличии данные. Математически это можно представить как:
![]()
В отличие от частотного подхода, Байесовская статистика работает с неопределенностью через достоверные интервалы (credible interval), которые интуитивно понятны. 95% достоверный интервал означает, что значение измеряемого параметра попадает в него с 95% вероятностью.
В этой ветке статистики все крутится вокруг теоремы, позволяющей рассчитать условные вероятности исходя из накопленных знаний:
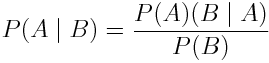
Несмотря на кажущуюся простоту, Теорема Байеса имеет огромную ценность, она применяется в различных областях, и даже существует отдельная ветвь статистики, которая называется Байесовская статистика. Если интересно понять, как выводится эта формула, то вот ссылка на отличный пост, посвященный Теореме Байеса.
Распределения
Распределение вероятностей – это закон, описывающий вероятности наступления всех возможных исходов какой-либо случайной величины, выраженных в виде математической функции. Как и любая функция, распределение может обладать параметрами, позволяющими скорректировать его характеристики.
Когда мы измеряли относительную частоту исходов такого события как подбрасывание монеты, мы на самом деле рассчитали так называемое эмпирическое распределение вероятностей. Многие процессы, отличающиеся неопределенностью, могут быть описаны в терминах распределения вероятностей. Так, например, подбрасывание монеты описывается распределением Бернулли, а если бы мы захотели рассчитать вероятность, что после n попыток выпадет орел, мы можем прибегнуть к Биномиальному распределению.
Для удобства работы с вероятностями введем новое понятие, аналогичное переменной, - случайная переменная. Каждая случайная переменная соответствует определенному распределению. Случайные величины принято обозначать заглавной буквой, а также мы можем использовать символ ~, чтобы обозначить, какому распределению соответствует переменная.
Это означает, что случайная переменная X описывается распределением Бернулли, при этом вероятность успеха (выпадение орла) равна 0,6.
Непрерывное и дискретное распределение вероятностей
Распределения вероятностей бывают двух типов. Дискретное распределение описывает случайные величины, которые принимают конечное число значений, как это было в примере с монетой и распределением Бернулли. Дискретные распределения определяются Функцией распределения масс (Probability Mass Function). Непрерывное распределение описывает непрерывные случайные величины, которые (в теории) могут принимать бесчисленное число значений. Например, когда мы измеряем скорость и ускорение датчиками с высокими шумами. Непрерывные распределения определяются Функцией плотности распределения вероятности (Probability Density Function).
При расчете статистик для дискретного распределения вероятностей применяется суммирование ∑, а для непрерывного – интегралы ∫. Например, математическое ожидание будет иметь следующий вид:


Выборки и статистики
Представим, что мы хотим измерить рост людей в своем городе. Чтобы измерения были независимыми, мы оценивали рост случайных прохожих на улице. Процесс случайного отбора подмножества данных из общей (генеральной) совокупности называется выборкой.
Выборка сама по себе достаточно сложна для понимания. Для того, чтобы описать ее более понятным для человека способом используются статистические показатели – обобщающие математические функции.
С одним таким показателем вы скорее всего уже сталкивались – это арифметическое среднее.
Другой пример – это дисперсия выборки:
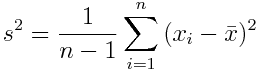
Данная формула характеризует разброс значений в массиве данных относительно среднего.
А если я хочу узнать больше?
Знания статистики могут пригодиться в самых неочевидных ситуациях. Как сказал известный статист Джон Тьюки: “The best thing about being a statistician is that you get to play in everyone's backyard”.
Вот небольшая подборка ресурсов для продолжения изучения математической статистики:
· Начинающие: Академия Khan – это отличный бесплатный ресурс. Их курс даст вам представление об основах теории вероятностей и статистики простым и понятным языком.
· Средний уровень: Учебник Ларри Вассермана All of the statistics представляет собой отличный обзор всех наиболее важных вопросов статистики в сжатой форме. Но имейте в виду, эта книга рассчитана на читателей, уже знакомых с линейной алгеброй и математическим анализом.
· Продвинутый уровень: Предположу, что, дойдя до этого этапа, вы уже составите свой собственный список литературы